Lecture 16 - Deep Learning from a GM Perspective

Deep learning foundations viewed through the lens of graphical models, covering perceptrons, neural networks, backpropagation, and probabilistic interpretations.

Logistics Review

• Class webpage: lengerichlab.github.io/pgm-spring-2025
• Lecture scribe sign-up sheet
• Readings,Class Announcements, Assignment Submissions: Canvas
• Instructor: Ben Lengerich
  • Office Hours: Thursday 3:30-4:30pm, 7278 Medical Sciences Center
  • Email: lengerich@wisc.edu
• TA: Chenyang Jiang
  • Office Hours: Monday 11am-12pm, 1219 Medical Sciences Center
  • Email: cjiang77@wisc.edu
• Module 3: Suggested focusing more on papers (or youtube vedios)

Graded material

• Exam (20%, grades TBD)
• Project midterm report (5%, 4/11)
• Project presentation (5%, 4/31, 5/1)
  • Sign up here!
• Project final report (15%, 5/5)
• Extra credit (3%, sign-up)

About Research Papers

While research papers may appear rigorous and comprehensive, they often omit practical nuances. As learners, we should approach them optimistically — extracting value even from imperfect sources.

---

From Biological to Artificial Neurons

Early AI models were inspired by biological neurons. The McCulloch & Pitts neuron, proposed in 1943, used threshold logic to compute simple Boolean functions like AND and OR. However, it could not represent XOR.

---

The Perceptron and Its Limits

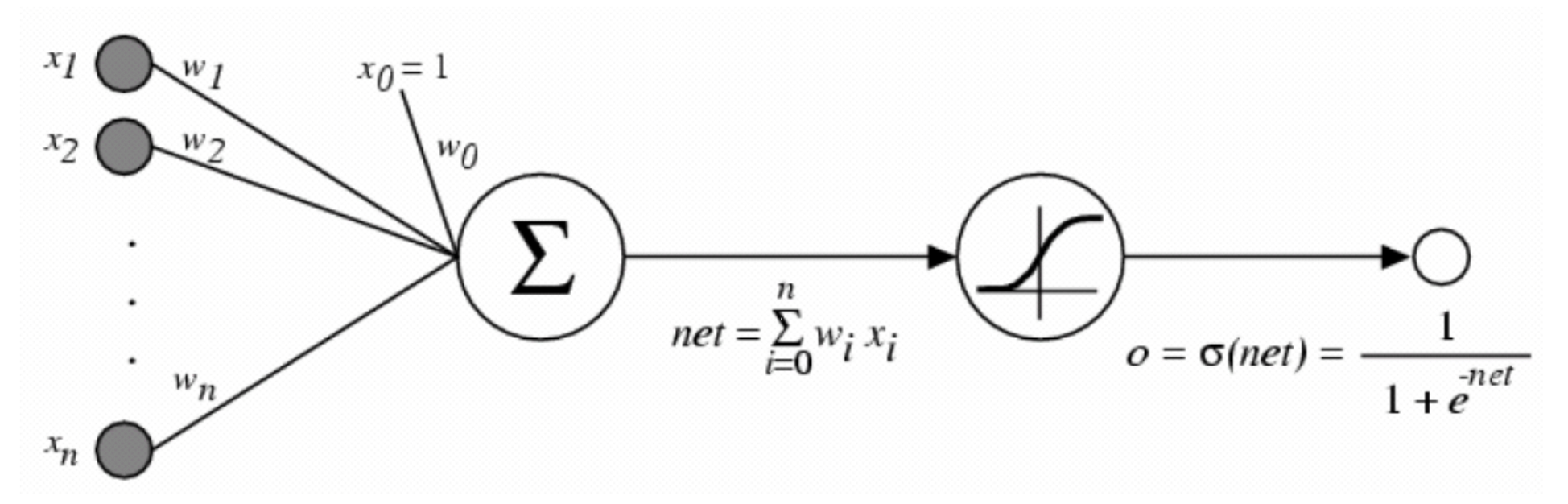
The perceptron extended MP neurons by introducing weighted inputs and activation functions (like sigmoid):

f(x) = \sigma(w^\top x + b)

This model supports gradient-based learning for functions like:

Y \sim \mathcal{N}(f(x), \Sigma) \Rightarrow \arg\min_w \sum_i \left(y_i - f(x_i; w)\right)^2

Why XOR Cannot Be Represented

Suppose XOR could be represented by a single-layer perceptron. Then:

for input (1,1):

\sigma(w_1 + w_2) < \theta

for input (1,0), (0,1):

\sigma(w_1) \geq \theta , \sigma(w_2) \geq \theta

Adding the latter two contradicts the first — no linear decision boundary exists.

---

Multi-Layer Perceptrons (MLP)

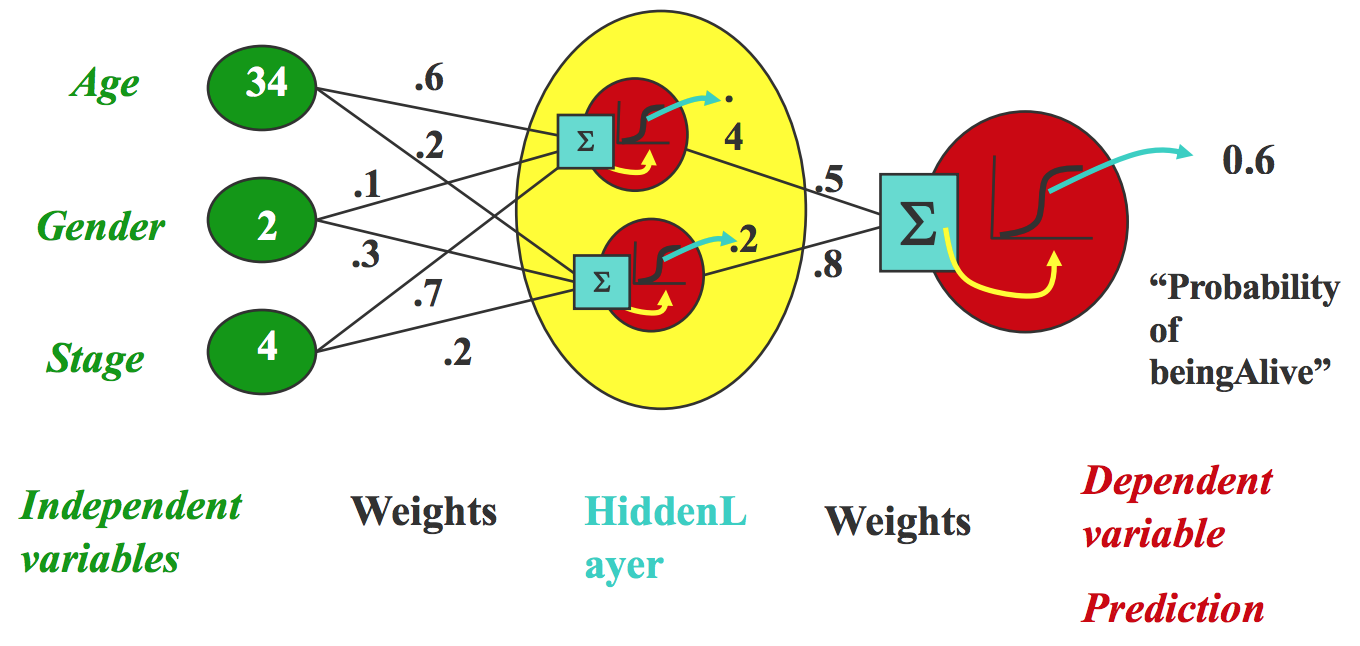
To model non-linear functions like XOR, multi-layer perceptrons are introduced:

• Input Layer:

x

• Hidden Layer(s):

h = \sigma(Wx + b)

• Output Layer:

\hat{y} = W' h + b'

This architecture allows hierarchical feature extraction and can represent any continuous function under mild assumptions.

---

Backpropagation

Neural networks are compositions of differentiable functions:

L = \ell(f_3(f_2(f_1(x))))

The gradient is computed via reverse-mode autodiff:

\frac{dL}{dx} = \frac{dL}{df_3} \cdot \frac{df_3}{df_2} \cdot \frac{df_2}{df_1} \cdot \frac{df_1}{dx}

This process is the core of backpropagation, enabling scalable training of deep networks.

---

Graphical Models vs. Deep Nets

Graphical Models (GMs)	Deep Neural Networks (DNNs)
Probabilistic semantics	Function approximation
Explicit latent variables	Learned intermediate features
Inference via message passing	Learning via SGD

While GMs offer interpretability, DNNs provide flexibility and scalability. Hybrid models aim to combine both strengths.

---

Probabilistic Neural Nets

Restricted Boltzmann Machines (RBM)

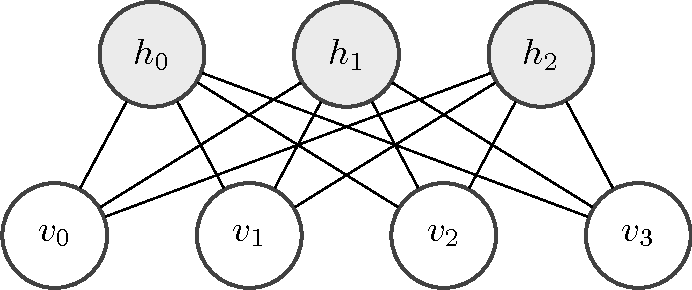
An RBM is an undirected graphical model with visible ( v ) and hidden ( h ) units:

P(v, h) \propto e^{-E(v, h)}, \quad E(v, h) = -v^\top W h - a^\top v - b^\top h

RBMs are trained using contrastive divergence, and serve as building blocks for deeper models.

---

Deep Belief Networks (DBN)

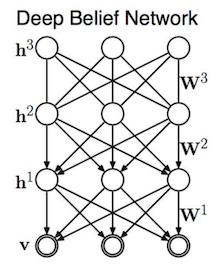
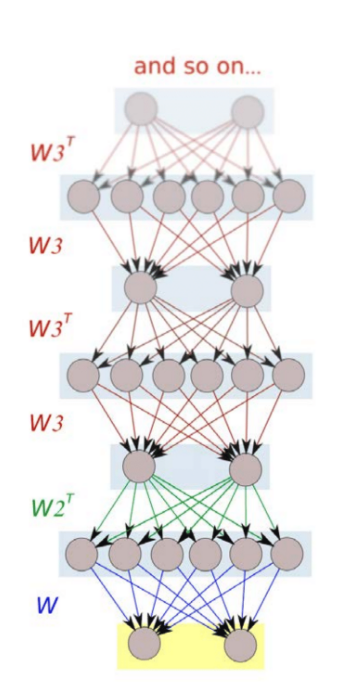
DBNs stack multiple RBMs and apply layer-wise pretraining, followed by supervised fine-tuning. They offer a probabilistic view of deep learning, with each layer capturing increasingly abstract representations.

---

NNs and GMs—Natural Complements

Neural networks and graphical models represent two major paradigms in probabilistic AI. While they originate from different modeling philosophies, they can be viewed as complementary in both function and design.

Graphical models (GMs) offer structured representations of joint distributions, with explicit semantics over variables and their dependencies. In contrast, neural networks (NNs) are powerful function approximators, trained end-to-end via gradient-based optimization. Despite this apparent contrast, many modern systems integrate the two:

• GMs for interpretability, NNs for flexibility: GMs allow for explicit latent structure and reasoning under uncertainty, while NNs can model complex, high-dimensional mappings without handcrafted features.

• Neural modules within probabilistic models: In structured prediction, NNs can be used to parameterize potentials in conditional random fields (CRFs), or emission probabilities in HMMs.

• Probabilistic perspectives on NNs: Some architectures (e.g., RBMs, DBNs) are inherently graphical models, and even standard feedforward networks can be viewed as approximate inference in layered latent variable models.

• Uncertainty estimation in NNs: Probabilistic modeling techniques such as variational inference or Bayesian dropout can be used to quantify uncertainty in neural predictions, a critical aspect in safety-sensitive domains.

Specific examples include:

• Collobert & Weston, 2011 combined recurrent neural networks with probabilistic decoding in speech recognition, using RNNs for acoustic modeling and probabilistic search for decoding.

• Toosi et al., 2021 applied deep networks to NLP tasks, where word embeddings are learned by a neural network, and structured output is modeled using CRFs.

Ultimately, the synergy between GMs and NNs enables systems that are both expressive and interpretable.

---